在推荐系统领域，矩阵分解（Matrix Factorization）和因子分解机（Factorization Machines, FM）是两种广泛应用的技术，尤其在处理稀疏数据和隐式反馈方面表现优异。本文将结合Datawhale推荐系统任务三的内容，详细介绍矩阵分解与FM模型的原理、应用及其在推荐系统中的实现方式。

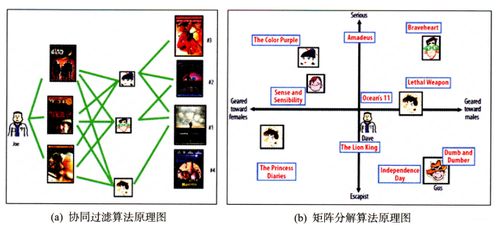
一、矩阵分解模型

矩阵分解的核心思想是将用户-物品交互矩阵分解为两个低维矩阵的乘积，分别代表用户和物品的隐向量。通过这种分解，可以预测用户对未交互物品的评分或偏好。常见的矩阵分解方法包括奇异值分解（SVD）及其变种（如FunkSVD、BiasSVD）。矩阵分解能够有效挖掘用户和物品的潜在特征，缓解数据稀疏性问题，并提升推荐的准确性和多样性。

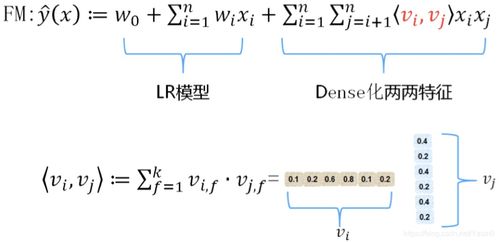
二、因子分解机（FM）模型

因子分解机是一种通用的监督学习算法，特别适用于处理高维稀疏数据，如推荐系统中的用户-物品交互特征。FM模型不仅考虑特征的线性组合，还通过隐向量内积捕捉特征之间的交互关系。与传统的矩阵分解相比，FM可以灵活地融入多种特征（如用户属性、物品属性、上下文信息），从而更全面地建模用户行为。FM的公式简洁高效，能够在线性时间内计算预测结果，适合大规模推荐场景。

三、矩阵分解与FM在推荐系统中的结合应用

在实际推荐系统中，矩阵分解和FM常被结合使用。例如，可以将矩阵分解得到的用户和物品隐向量作为FM的输入特征，进一步增强模型的表达能力。通过这种方式，系统能够同时利用协同过滤信息和辅助特征，提高推荐性能。FM还可以用于处理冷启动问题，通过引入新用户或物品的属性特征来生成初始推荐。

四、实现与优化

在Datawhale的task3中，学习者通常通过Python库（如Surprise或PyTorch）实现矩阵分解和FM模型。关键步骤包括数据预处理、模型训练、超参数调优和评估（如使用RMSE或Precision@K指标）。优化方法可能涉及随机梯度下降（SGD）或交替最小二乘法（ALS），以最小化预测误差。

矩阵分解和FM是推荐系统中强大的工具，它们通过挖掘潜在特征和特征交互，有效提升了推荐的准确性和鲁棒性。掌握这些技术，有助于构建更智能、个性化的推荐系统。